這里“MM”-馬爾可夫模型,不是跟中國網絡俗語“美眉”有關，而是跟俄國的“老司機”馬爾可夫有關。

這位“老司機”全名叫安德雷·安德耶維齊·馬爾可夫（Андрей Андреевич Марков），是俄國數學家。1874年18歲的馬爾可夫考入圣彼得堡大學，師從切比雪夫（另一位俄國“老司機”，著名的切比雪夫定理-概率論與數理統計的基礎），物理-數學博士，畢業后留校任教，圣彼得堡大學教授，圣彼得堡科學院院士。在概率論、數論、函數逼近論和微分方程等方面卓有成就。

馬爾可夫模型概述：

馬爾可夫模型MM（MarkovModel）是一種統計模型。它的原始模型馬爾可夫鏈，由俄國數學家馬爾可夫于1906年提出，將此一般化到可數無限狀態空間是由柯爾莫果洛夫在1936年給出的。馬爾可夫鏈是與馬爾可夫過程緊密相關。馬爾可夫過程是研究離散事件動態系統狀態空間的重要方法，它的數學基礎是隨機過程理論。

馬爾可夫性質：

此性質稱為馬爾可夫性質（Markov Property），亦稱無后效性或無記憶性。

若X(t)為離散型隨機變量，則馬爾可夫性亦滿足等式。

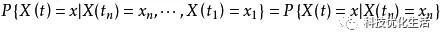
馬爾可夫過程：

若隨機過程{X(t), t屬于T}滿足馬爾可夫性質，則稱為馬爾可夫過程。

比如，荷花池中一只青蛙的跳躍，液體中微粒所作的布朗運動，傳染病受感染的人數，原子核中一自由電子在電子層中的跳躍，人口增長過程、闖迷宮的老鼠等都可視為馬爾可夫過程。

常見馬爾可夫過程有：

(1)獨立隨機過程為馬爾可夫過程。

(2)獨立增量過程為馬爾可夫過程。

(3)泊松過程為馬爾可夫過程。

(4)維納過程為馬爾可夫過程。

(5)質點隨機游動過程為馬爾可夫過程。

跟樸素貝葉斯、支持向量機等機器學習算法不同，馬爾可夫過程不必給處理的數據打標簽。馬爾可夫過程更側重于處理控制或決策問題。

馬爾可夫過程用于預測基本步驟：首先確定系統狀態,然后確定狀態之間轉移概率,再進行預測,并對預測結果進行分析-若結果合理,則可提交預測報告,否則需檢查系統狀態及狀態轉移概率是否正確。

馬爾可夫鏈：

馬爾可夫鏈MC（Markov Chain）是指數學中具有馬爾可夫性質的離散事件隨機過程。該過程中，在給定當前知識或信息的情況下，過去對于預測將來是無關的。在馬爾可夫鏈的每一步，系統根據概率分布，可以從一個狀態變到另一個狀態，也可以保持當前狀態。狀態的改變叫做轉移，與不同的狀態改變相關的概率叫做轉移概率。

時間和狀態都離散的馬爾可夫過程成為馬爾可夫鏈MC。

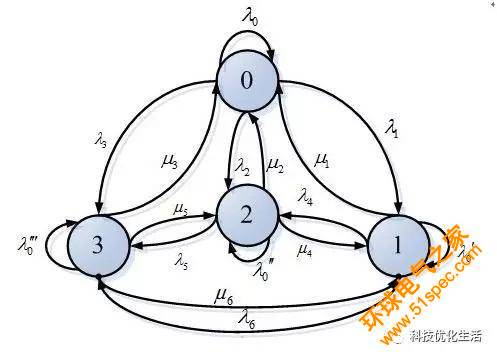
馬爾可夫鏈原理：

馬爾可夫鏈MC描述了一種狀態序列，其每個狀態值取決于前面有限個狀態。馬爾可夫鏈是具有馬爾可夫性質的隨機變量的一個數列。這些變量的范圍，即它們所有可能取值的集合，被稱為“狀態空間”，而的值則是在時間n的狀態。

馬爾可夫鏈是與馬爾可夫過程緊密相關。運用馬爾可夫鏈只需要最近或現在的動態資料便可預測將來。

馬爾可夫鏈性質：

馬爾可夫鏈MC具有以下性質：

1）正定性：狀態轉移矩陣中的每一個元素被稱為狀態轉移概率，由概率論知識可知，每個狀態轉移概率皆為正數，用公式即可表示為：

2）有限性：由概率論知識知，狀態轉移陣中的每一行狀態轉移陣中每行相加皆為1，用公式可表示為:

馬爾可夫序列分類器：

序列分類器或序列標號器是給序列中的某個單元指派類或者標號的模型。諸如：詞類標注、語音識別、句子切分、字素音位轉換、局部句法剖析、語塊分析、命名實體識別、信息抽取都屬于序列分類。

馬爾可夫序列分類器為：

1）顯馬爾可夫模型（VMM），又叫馬爾可夫模型MM。

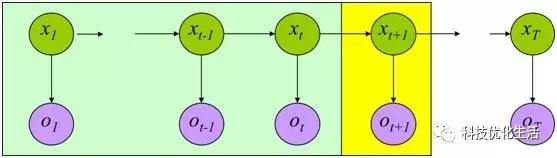
2）隱馬爾可夫模型（HMM）,描述一個含有隱含未知參數的馬爾可夫過程，是一個雙重隨機過程（包括馬爾可夫鏈和一般隨機過程）。

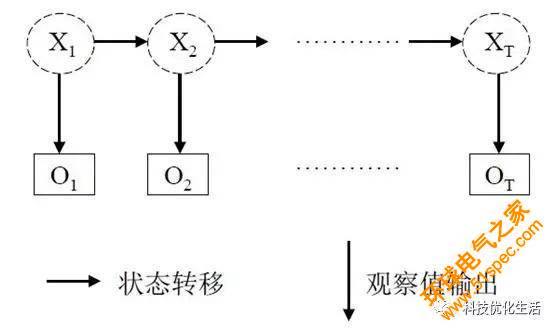
馬爾可夫模型應用：

馬爾可夫模型廣泛應用在語音識別，詞性自動標注，音字轉換，概率文法等各個自然語言處理、算術編碼、地理統計學、企業產品市場預測、人口過程、生物信息學（編碼區域或基因預測）等應用領域。經過長期發展，尤其是在語音識別中的成功應用，使它成為一種通用的統計工具。

1）狀態統計建模：馬爾可夫鏈通常用來建模排隊理論和統計學中的建模。還可作為信號模型用于熵編碼技術等。馬爾科夫鏈預測法是一種適用于隨機過程的科學、有效的動態預測方法。馬爾可夫鏈有眾多的生物學應用，特別是人口過程，可以幫助模擬生物人口過程的建模。

2）隱蔽馬爾可夫模型（HMM）還被用于生物信息學，用以編碼區域或基因預測。1980年代后半期，HMM開始應用到生物序列尤其是DNA的分析中。此后，在生物信息學領域HMM逐漸成為一項不可或缺的技術。到目前為止，隱馬爾可夫模型（HMM）一直被認為是實現快速精確的語音識別系統的最成功的方法。復雜的語音識別問題通過隱含馬爾可夫模型能非常簡單地被表述、解決，讓人們由衷地感嘆數學模型之妙。

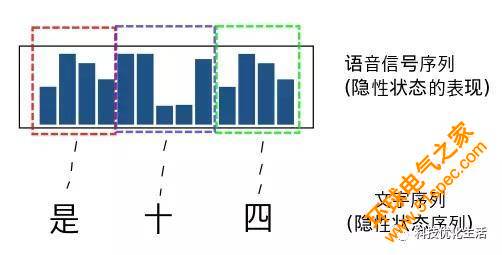
3）馬爾科夫鏈蒙特卡羅方法（Markov Chain Monte Carlo）方法: 馬爾科夫鏈蒙特卡羅MCMC是在樸素貝葉斯[請參見公眾號“科技優化生活”之人工智能（29）]論框架下，通過計算機進行模擬的蒙特卡羅方法[請參見公眾號“科技優化生活”之人工智能（31）]，該方法將馬爾科夫鏈(MC)引入到蒙特卡羅（MC）模擬中，實現隨著抽樣分布隨機模擬的進行而改變的動態模擬，彌補了傳統的蒙特卡羅積分只能靜態模擬的缺陷，是近年來廣泛應用的統計計算方法。

結語:

馬爾可夫模型（Markov Model）是一種統計模型。它的原始模型馬爾可夫鏈，由俄國數學家馬爾可夫于1906年提出。運用馬爾可夫鏈只需要最近或現在的動態資料便可預測將來。馬爾可夫鏈是與馬爾可夫過程緊密相關。馬爾可夫過程是研究離散事件動態系統狀態空間的重要方法，它的數學基礎是隨機過程理論。馬爾可夫模型在及人工智能之自然語言處理等領域應用廣泛。

原創   張志榮