人工智能機(jī)器學(xué)習(xí)有關(guān)算法內(nèi)容，請(qǐng)參見(jiàn)公眾號(hào)“科技優(yōu)化生活”之前相關(guān)文章。人工智能之機(jī)器學(xué)習(xí)主要有三大類(lèi)：1）分類(lèi)；2）回歸；3）聚類(lèi)。今天我們重點(diǎn)探討一下CART算法。 

繼上兩篇決策樹(shù)算法之ID3算法［參見(jiàn)人工智能（41）］和ID3的改進(jìn)算法－C4．5算法［參見(jiàn)人工智能（42）］后，本文繼續(xù)討論另一種二分決策樹(shù)算法－CART算法。我們知道十大機(jī)器學(xué)習(xí)中決策樹(shù)算法占有兩席位置，即C4．5算法和CART算法，可見(jiàn)CART算法的重要性。下面重點(diǎn)介紹CART算法。

不同于ID3與C4．5，CART為一種二分決策樹(shù)，是滿(mǎn)二叉樹(shù)。CART算法由Breiman等人在 1984 年提出，它采用與傳統(tǒng)統(tǒng)計(jì)學(xué)完全不同的方式構(gòu)建預(yù)測(cè)準(zhǔn)則，它是以二叉樹(shù)的形式給出，易于理解、使用和解釋。由CART 模型構(gòu)建的預(yù)測(cè)樹(shù)在很多情況下比常用的統(tǒng)計(jì)方法構(gòu)建的代數(shù)學(xué)預(yù)測(cè)準(zhǔn)則更加準(zhǔn)確，且數(shù)據(jù)越復(fù)雜、變量越多，算法的優(yōu)越性就越顯著。

CART算法既可用于分類(lèi)也可用于回歸。CART算法被稱(chēng)為數(shù)據(jù)挖掘領(lǐng)域內(nèi)里程碑式的算法。

CART算法概念：

CART（Classification andRegression Tree） 分類(lèi)回歸樹(shù)是一種決策樹(shù)構(gòu)建算法。CART是在給定輸入隨機(jī)變量X條件下輸出隨機(jī)變量Y的條件概率分布的學(xué)習(xí)方法。CART假設(shè)決策樹(shù)是二叉樹(shù)，內(nèi)部結(jié)點(diǎn)特征的取值為“是”和“否”，左分支是取值為“是”的分支，右分支是取值為“否”的分支。這樣的決策樹(shù)等價(jià)于遞歸地二分每個(gè)特征，將輸入空間即特征空間劃分為有限個(gè)單元，并在這些單元上確定預(yù)測(cè)的概率分布，也就是在輸入給定的條件下輸出的條件概率分布。

CART算法既可以處理離散型問(wèn)題，也可以處理連續(xù)型問(wèn)題。這種算法在處理連續(xù)型問(wèn)題時(shí)，主要通過(guò)使用二元切分來(lái)處理連續(xù)型變量，即特征值大于某個(gè)給定的值就走左子樹(shù)，或者就走右子樹(shù)。

CART算法組成：

CART算法組成如下：

1）決策樹(shù)生成：基于訓(xùn)練數(shù)據(jù)集生成決策樹(shù)，生成的決策樹(shù)要盡量大；自上而下從根開(kāi)始建立節(jié)點(diǎn)，在每個(gè)節(jié)點(diǎn)處要選擇一個(gè)最好（不同算法使用不同指標(biāo)來(lái)定義＂最好＂）的屬性來(lái)分裂，使得子節(jié)點(diǎn)中的訓(xùn)練數(shù)據(jù)集盡量的純。

2）決策樹(shù)剪枝：用驗(yàn)證數(shù)據(jù)集對(duì)已生成的樹(shù)進(jìn)行剪枝并選擇最優(yōu)子樹(shù)，這時(shí)損失函數(shù)最小作為剪枝的標(biāo)準(zhǔn)。這里用代價(jià)復(fù)雜度剪枝CCP（Cost－Complexity Pruning）。

決策樹(shù)的生成就是通過(guò)遞歸地構(gòu)建二叉決策樹(shù)的過(guò)程，對(duì)回歸樹(shù)用平方誤差最小化準(zhǔn)則，對(duì)分類(lèi)樹(shù)用基尼指數(shù)最小化準(zhǔn)則，進(jìn)行特征選擇，生成二叉樹(shù)。

CART決策樹(shù)生成：

1）回歸樹(shù)生成

回歸樹(shù)采用均方誤差作為損失函數(shù)，樹(shù)生成時(shí)會(huì)遞歸的按最優(yōu)特征與最優(yōu)特征下的最優(yōu)取值對(duì)空間進(jìn)行劃分，直到滿(mǎn)足停止條件為止，停止條件可以人為設(shè)定，比如當(dāng)切分后的損失減小值小于給定的閾值 ε，則停止切分，生成葉節(jié)點(diǎn)。對(duì)于生成的回歸樹(shù)，每個(gè)葉節(jié)點(diǎn)的類(lèi)別為落到該葉節(jié)點(diǎn)數(shù)據(jù)的標(biāo)簽的均值。

回歸樹(shù)為一棵二叉樹(shù)，每次都是按特征下的某個(gè)取值進(jìn)行劃分，每一個(gè)內(nèi)部節(jié)點(diǎn)都是做一個(gè)對(duì)應(yīng)特征的判斷，直至走到葉節(jié)點(diǎn)得到其類(lèi)別，構(gòu)建這棵樹(shù)的難點(diǎn)在于如何選取最優(yōu)的切分特征與切分特征對(duì)應(yīng)的切分變量。

回歸樹(shù)與模型樹(shù)既可以處理連續(xù)特征也可以處理離散特征。

回歸樹(shù)生成算法如下：

輸入：訓(xùn)練數(shù)據(jù)集 D＝｛（x1，y1），（x2，y2），…，（xN，yN）｝

輸出：回歸樹(shù) T

1）求解選擇切分特征 j 與切分特征取值 s ，j 將訓(xùn)練集 D 劃分為兩部分，R1 與R2 ，依照（j，s）切分后如下：

R1（j，s）＝｛xi｜xji≤s｝   R2（j，s）＝｛xi｜xji＞s｝

c1＝1N1∑xi∈R1yi    c2＝1N2∑xi∈R2yi

2）遍歷所有可能的解（j，s），找到最優(yōu)的 （j＊，s＊） ，最優(yōu)的解使得對(duì)應(yīng)損失最小，按照最優(yōu)特征（j＊，s＊）來(lái)切分即可。

Min ｛ ∑ （yi–c1）＾2 ＋∑ （yi–c2）＾2 ｝

j，s    xi∈R1          xi∈R2

3）遞歸調(diào)用 1）和2），直到滿(mǎn)足停止條件。

4）返回決策樹(shù) T。

回歸樹(shù)主要采用了分治策略，對(duì)于無(wú)法用唯一的全局線(xiàn)性回歸來(lái)優(yōu)化的目標(biāo)進(jìn)行分而治之，進(jìn)而取得比較準(zhǔn)確的結(jié)果，但分段取均值并不是一個(gè)明智的選擇，可以考慮將葉節(jié)點(diǎn)設(shè)置為一個(gè)線(xiàn)性函數(shù)，這便是所謂的分段線(xiàn)性模型樹(shù)。實(shí)驗(yàn)表明：模型樹(shù)效果比回歸樹(shù)的效果要好一些。模型樹(shù)只需在回歸樹(shù)的基礎(chǔ)上稍加修改即可，對(duì)于分到葉節(jié)點(diǎn)的數(shù)據(jù)，采用線(xiàn)性回歸的最小均方損失來(lái)計(jì)算該節(jié)點(diǎn)的損失。

2）分類(lèi)樹(shù)生成

分類(lèi)樹(shù)是CART中用來(lái)分類(lèi)的，不同于 ID3 與 C4．5，CART分類(lèi)樹(shù)采用基尼指數(shù)來(lái)選擇最優(yōu)的切分特征，而且每次都是二分。

基尼指數(shù)是一個(gè)類(lèi)似與熵的概念，對(duì)于一個(gè)有 K 種狀態(tài)對(duì)應(yīng)的概率為 p1，p2，…，pK的隨機(jī)變量 X ，其基尼指數(shù)Gini定義如下：

Gini（X）＝∑pk（1？pk）＝1？∑kp2k

k                       k

在已知特征 A條件下集合 D 的基尼指數(shù)：

Gini（D，A）＝（｜D1｜／｜D｜）＊Gini（D1）＋（｜D2｜／｜D｜）＊Gini（D2）

Gini（D，A）取值越大，樣本的不確定性也越大，這一點(diǎn)與熵類(lèi)似，所以選擇特征 A 的標(biāo)準(zhǔn)是 Gini（D，A） 的取值越小越好。

分類(lèi)樹(shù)生成算法如下：

輸入：訓(xùn)練數(shù)據(jù)集 D＝｛（x1，y1），（x2，y2），…，（xN，yN）｝，停止條件

輸出：分類(lèi)樹(shù) T

1）利用特征 A 的取值 a 將數(shù)據(jù)分為兩部分，計(jì)算 A＝a時(shí)的基尼系數(shù)：

Gini（D，A）＝（｜D1｜／｜D｜）＊Gini（D1）＋（｜D2｜／｜D｜）＊Gini（D2）

2）對(duì)整個(gè)數(shù)據(jù)集中所有的可能特征 A 以及其可能取值 a 選取基尼系數(shù)最小的特征 A＊ 與特征下的取值 a＊，來(lái)將數(shù)據(jù)集切分，將數(shù)據(jù) D1、D2 分到兩個(gè)子節(jié)點(diǎn)中去。

3）對(duì)子節(jié)點(diǎn)遞歸調(diào)用 1）和2） ，直至滿(mǎn)足停止條件

4）返回 CART 樹(shù) T

該算法停止條件可以是節(jié)點(diǎn)中的樣本數(shù)不能小于給定閾值，或者樣本集的基尼系數(shù)小于給定閾值，或者沒(méi)有更多的特征。

3）剪枝

CART需要對(duì)生成的樹(shù)進(jìn)行剪枝，避免模型過(guò)度擬合訓(xùn)練數(shù)據(jù)，剪枝時(shí)使用的損失函數(shù)如下：

Ca（T）＝C（T）＋a｜T｜

C（T）為樹(shù) T 對(duì)訓(xùn)練數(shù)據(jù)的誤差，可以用基尼系數(shù)或者均方損失來(lái)表示，a≥0 代表一個(gè)權(quán)衡訓(xùn)練數(shù)據(jù)損失 C（T）與總節(jié)點(diǎn)數(shù) ｜T｜的參數(shù)，Ca（T） 代表了樹(shù) T 的整體損失，對(duì)于固定的 a，一定存在一個(gè)確定的使得 Ca（T）最小的子樹(shù)，當(dāng) a偏大時(shí)， ｜T｜ 偏小，樹(shù) T 的規(guī)模偏小，反之，樹(shù) T 的規(guī)模偏大，Breiman 等人采用遞歸的方法對(duì) CART 進(jìn)行剪枝，將 a從小增大  0＝a0＜a1＜…＜an，如此產(chǎn)生的區(qū)間 a∈［ai，ai＋1）， i＝1，2，…，n用對(duì)應(yīng)此區(qū)間的 a 產(chǎn)生一系列的子樹(shù)序列 ｛T0，T1，…，Tn｝這里 Ti＋1總是由 Ti 剪枝后產(chǎn)生。

剪枝算法如下：

輸入：CART 生成樹(shù) T0

輸出：剪枝后的最優(yōu)樹(shù) T＊

1）設(shè) k＝0 ， T＝T0 ，a＝＋∞

3） 自下而上的對(duì)內(nèi)部節(jié)點(diǎn) t 計(jì)算：

g（t）＝［Ct？C（Tt）］／（｜Tt｜？1）

a＝min（a，g（t））

4） 自上而下的訪問(wèn)內(nèi)部節(jié)點(diǎn) t ，對(duì)最小的 g（t）＝a進(jìn)行剪枝，并對(duì)葉節(jié)點(diǎn) t 以多數(shù)表決形式?jīng)Q定其類(lèi)別，得到樹(shù) T

5） k＝k＋1， ak＝a，Tk＝T

6） 如果 T 為非單節(jié)點(diǎn)樹(shù)，回到4）

7） 對(duì)于產(chǎn)生的子樹(shù)序列 ｛T0，T1，…，Tn｝分別計(jì)算損失，得到最優(yōu)子樹(shù) T＊并返回．

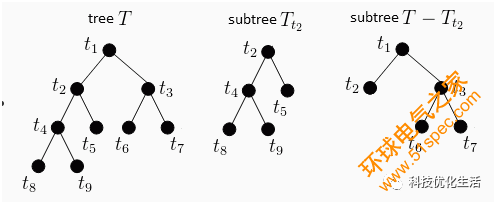
剪枝后的樹(shù)便是所需要的CART決策樹(shù)。

CART優(yōu)點(diǎn)：

1） 可以生成可以理解的規(guī)則；

2） 計(jì)算量相對(duì)來(lái)說(shuō)不是很大；

3） 可以處理連續(xù)和種類(lèi)字段；

4）決策樹(shù)可以清晰的顯示哪些字段比較重要。

CART缺點(diǎn)：

1） 對(duì)連續(xù)性的字段比較難預(yù)測(cè)；

2） 對(duì)有時(shí)間順序的數(shù)據(jù)，需要很多預(yù)處理的工作；

3）當(dāng)類(lèi)別太多時(shí)，錯(cuò)誤可能就會(huì)增加的比較快；

4）一般的算法分類(lèi)的時(shí)候，只是根據(jù)一個(gè)字段來(lái)分類(lèi)。

CART應(yīng)用場(chǎng)景：

CART算法既可以處理離散型問(wèn)題，也可以處理連續(xù)型問(wèn)題。CART算法是一種非常有趣且十分有效的非參數(shù)分類(lèi)和回歸方法。它通過(guò)構(gòu)建二叉樹(shù)達(dá)到預(yù)測(cè)目的。它已在統(tǒng)計(jì)、數(shù)據(jù)挖掘和機(jī)器學(xué)習(xí)領(lǐng)域中普遍使用，是一種應(yīng)用廣泛的決策樹(shù)算法。

結(jié)語(yǔ)：

CART 模型最早由Breiman 等人提出，它采用與傳統(tǒng)統(tǒng)計(jì)學(xué)完全不同的方式構(gòu)建預(yù)測(cè)準(zhǔn)則，它是以二叉樹(shù)形式給出，易于理解、使用和解釋。由CART 模型構(gòu)建的預(yù)測(cè)樹(shù)在很多情況下比常用的統(tǒng)計(jì)方法構(gòu)建的代數(shù)學(xué)預(yù)測(cè)準(zhǔn)則更加準(zhǔn)確，且數(shù)據(jù)越復(fù)雜、變量越多，CART算法優(yōu)越性就越顯著。模型的關(guān)鍵是預(yù)測(cè)準(zhǔn)則的構(gòu)建。CART算法在統(tǒng)計(jì)、數(shù)據(jù)挖掘和機(jī)器學(xué)習(xí)等領(lǐng)域得到廣泛應(yīng)用。

－－－－－－以往文章推薦－－－－－－

機(jī)器學(xué)習(xí)

深度學(xué)習(xí)

人工神經(jīng)網(wǎng)絡(luò)

決策樹(shù)

隨機(jī)森林

強(qiáng)化學(xué)習(xí)

遷移學(xué)習(xí)

遺傳算法

樸素貝葉斯

支持向量機(jī)

蒙特卡羅方法

馬爾科夫模型

Hopfield神經(jīng)網(wǎng)絡(luò)

回歸模型

K鄰近算法

卷積神經(jīng)網(wǎng)絡(luò)

受限玻爾茲曼機(jī)

循環(huán)神經(jīng)網(wǎng)絡(luò)

長(zhǎng)短時(shí)記憶神經(jīng)網(wǎng)絡(luò)

Adaboost算法

ID3算法

C4．5算法